BIOGRAFÍA DE PITÁGORAS

La vida de Pitágoras se encuentra envuelta en leyendas. Nació en Jonia, en la isla de Samos, hacia el 572 a.C. y, al parecer, conoció a Anaximandro de Mileto. Se le atribuyen viajes a Egipto y Babilonia. La tiranía de Polícrates le hizo abandonar Samos, trasladándose a Italia y estableciéndose en Crotona. Allí creó una secta filosófico-religiosa, inspirada en el orfismo, cuyos miembros vivían en comunidad de bienes, participando de un conjunto de creencias y saberes que permanecían en secreto para los no iniciados.

La influencia ejercida por dicha secta en Crotona fue considerable, al parecer, llegando a suscitar la enemistad del pueblo que se rebeló contra el dominio ejercido por las secta pitagórica y, en el transcurso de esa revuelta popular, puso fuego a sus propiedades y los expulsó de la ciudad. Se dice que Pitágoras se refugió en Metaponto, donde murió poco después, hacia el 496 antes de Cristo.

Pensamiento

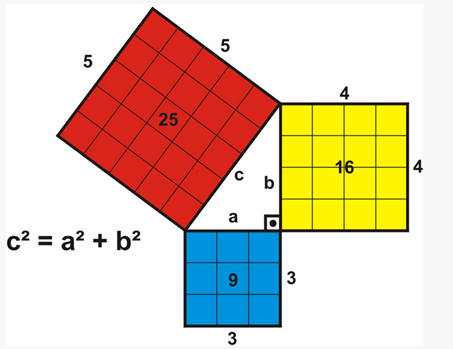
Son pocas las referencias a su obra entre los antiguos, incluidas las de Platón y Aristóteles, pero abundantes a partir de ellos (lo que genera muchas dudas sobre su autenticidad) y en las que se mezcla, además, la leyenda y la realidad, o lo que podría ser tomado como una referencia real a Pitágoras o a los pitagóricos (hoy sabemos, por ejemplo, que la atribución a Pitágoras del descubrimiento del teorema que lleva su nombre no es defendible). Es difícil fijar también qué doctrinas pertenecen a Pitágoras y cuáles pudieron ser desarrolladas por sus discípulos posteriores: Alcmeón o Filolao, por ejemplo.

La filosofía de Pitágoras se desarrolla en una doble vertiente: una místico-religiosa y otra matemático-científica.

a) Por lo que respecta a la primera, el eje central está representado por la teoría de la trasmigración de las almas y la consecuente afirmación del parentesco entre todos los seres vivos. Según ella, las almas son entidades inmortales que se ven obligadas a permanecer en cuerpos reencarnándose sucesivamente pasando de unos a otros durante un periodo de tiempo indeterminado, hasta superar el proceso de reencarnaciones gracias a la purificación (catarsis), que culmina en el regreso del alma a su lugar de origen. Para ello, era necesario observar numerosas reglas de purificación, por ejemplo, la abstinencia de la carne, así como diversas normas rituales y morales. Esta teoría será adaptada posteriormente por Platón, constituyendo un elemento importante de su filosofía.

b) Respecto a la vertiente matemático-científica, Pitágoras afirmaba que los números eran el principio (arjé) de todas las cosas.

b.1 No sabemos si se concebían los números como entidades físicas o si, por el contrario, se afirmaba que el principio de la realidad era algo de carácter formal, es decir, no material (una relación, una estructura...). Aristóteles pensaba que la doctrina pitagórica del número se basaba en descubrimientos empíricos; por ejemplo, el hecho de que los intervalos musicales puedan expresarse numéricamente. (De hecho los pitagóricos concedieron una gran importancia al estudio de la música, vista su relación con las matemáticas. Esta relación la pudieron ir ampliando al resto de objetos que constituyen la realidad, descubriendo en el número la razón de todo lo real, lo que llevaría a convertirlo en el "arjé" de los milesios.) Parece, además, que los pitagóricos concibieron los números espacialmente, identificando el punto geométrico con la unidad aritmética. Las unidades tendrían, pues, extensión espacial y podrían ser consideradas, como dice Aristóteles, como el elemento material de las cosas.

b.2 Es dudoso que los pitagóricos hayan podido interpretar el número como una realidad de carácter formal o como una estructura de la realidad, es decir, como algo no material, dado que la aparición clara de la concepción de una realidad no material difícilmente puede anticiparse a la reflexión platónica sobre el tema. No obstante, pese a las explicaciones de Aristóteles, tampoco queda muy claro cómo podría interpretarse el número como una entidad material. También en su vertiente matemática influirán en Platón los pitagóricos.

HIPOTENUSA

La hipotenusa es el lado opuesto al ángulo recto de un triángulo rectángulo. Es el lado mayor del triángulo rectángulo. Ésta puede calcularse a partir del teorema de Pitágoras a partir de los catetos.Siendo los catetos a y b, ésta se calculará por la fórmula siguiente:

CATETOS

Los catetos son los dos lados del triángulo rectángulo que forman el ángulo recto. El triángulo rectángulo tiene dos catetos. Estos se definen según el ángulo agudo de referencia a: Cateto adyacente (o contiguo): lado que forma el ángulo recto y es adyacente al ángulo a. Cateto opuesto: lado que forma el ángulo recto y opuesto al ángulo a. Si el ángulo de referencia no fuese el ángulo a sino que fuese el ángulo ß (el superior) los catetos adyacente y opuesto se invertirían.

DEMOSTRACION DE PITÁGORAS.

Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales. Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente. Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.

De la semejanza entre ABC y AHC:

y dos triángulos son semejantes si hay dos o más ángulos congruentes.

De la semejanza entre ABC y BHC:

Los resultados obtenidos son el teorema del cateto. Sumando:

Peropor lo que finalmente resulta:

Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.

Los triángulos PQR y PST son semejantes, de manera que:

siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:

obtenemos después de simplificar que:

obtenemos después de simplificar que:

pero siendo r la razón de semejanza, esta claro que:

Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".

Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:

que de acuerdo con las propiedades de las proporciones da:

y por la semejanza entre los triángulos ACH y ABC resulta que:

pero según (I) , asi que:

y por lo tanto:

quedando demostrado el teorema de Pitágoras.

Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.

Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados diferentes:

Uno de ellos –centro– está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.

El otro cuadrado –derecha– lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.

Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris () equivale a la de los cuadrados amarillo y azul (), habiéndose demostrado el teorema de Pitágoras.

EJERCICIOS.

Problema 1.
Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.

Problema 2. Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1cm, ¿cuánto mide el otro lado?

Problema 3. Calcular la hipotenusa del triángulo rectángulo cuyos lados miden y .

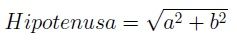
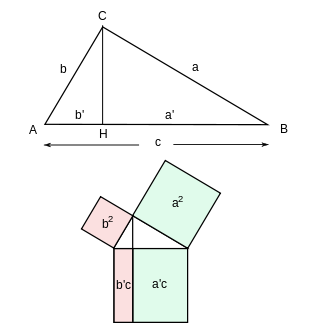
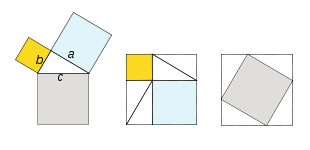
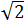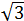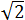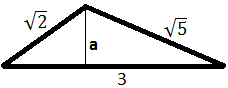
Problema 4. Calcular la altura del siguiente triángulo sabiendo que sus lados miden y 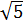y su base 3.

Problema 5. Calcular el perímetro del siguiente rombo si sabemos que sus diagonales(altura y anchura)miden 16 y 12.